Lecture #17

Chapter 14 starting with Section 2
(We'll return to Section 1 later)
  CURMUDGEON GENERAL'S WARNING. These "slides" represent highlights from lecture and are neither complete nor meant to replace lecture. It is advised not to use these as a reliable means to replace missed lecture material. Do so at risk to healthy academic performance in 09-105.
Lecture Outline (some material shown is look-and-listen only) Quantum Theory of the Chemical Bond

Molecular orbitals (in "homonuclear diatomic molecules"

Approximated by combinations of atomic orbitals

Constructive and destructive interference effects

Combining 1s atomic orbitals to get molecular orbitals

"Sigma" bonding molecular orbital

"Sigma" antibonding molecular orbital

Combining 2p atomic orbitals

"Sigma" bonding molecular orbital

"Sigma" antibonding molecular orbital

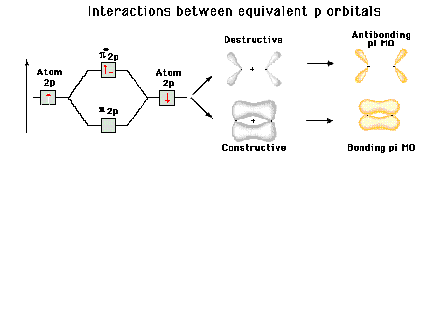
"Pi" bonding molecular orbitals

"Pi" antibonding molecular orbitals
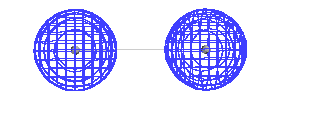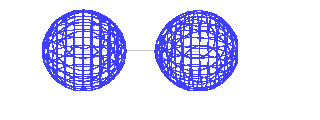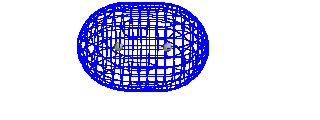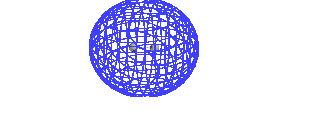
This is a calculated solution for the constructive interference result.
If destructive interference represents the orbital in which the electron happens to be found, the linear combination results in a depeletion of electron density between the positively charged protons. They repel each other under these circumstances.  
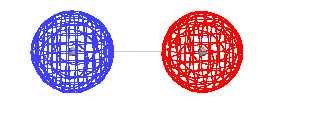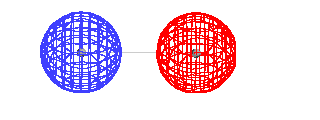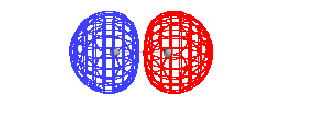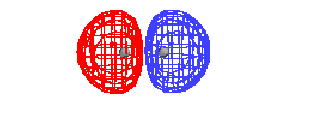
This is the destructive interference combination of 1s atomic orbitals
The total energy of the ground state of H2+ as a function of the distance between the protons.
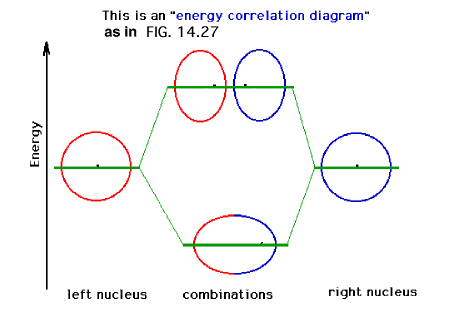
A schematic of the orbitals on separated protons relative to "close" protons. The constructive combination of atomic orbitals gives rise to a system lower in energy than the isolated system and is a bonding molecular orbital.  
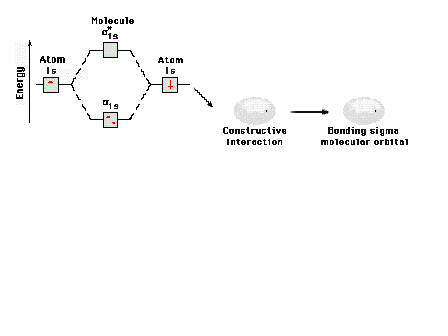
Energy diagram and geometry for the sigma-1s (bonding) orbital construction.
Energy diagram and geometry for the sigma*-1s (antibonding) orbital construction
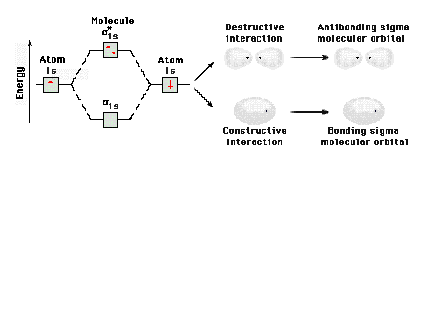Energy diagram and geometry for the sigma-2px (bonding) orbital construction from the 2p atomic orbitals originally directed along the bonding (x) axis.
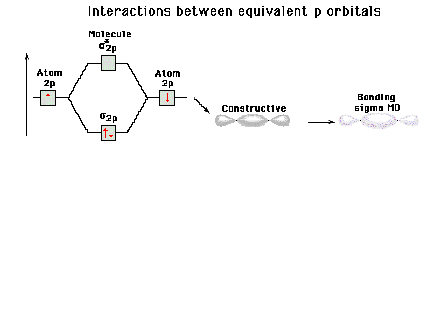This (with luck) is an animation of the computer-generated 2p (or p) bonding molecular orbital showing how the symmetry about the bond axis resembles that for the s-atomic orbital's symmetry about the nucleus. Hence the label.
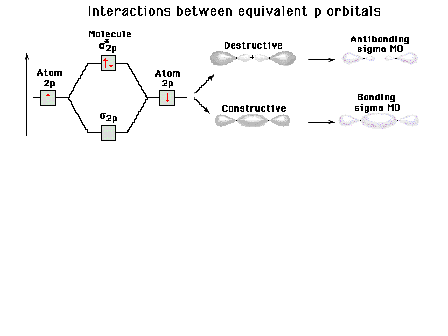
Energy diagram and geometry for the sigma*-2p (antibonding) molecular orbital construction
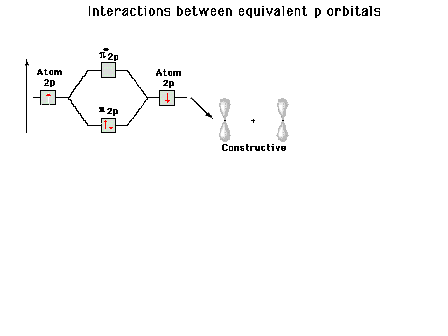
A reminder that, perpendicular to the bond axis in the x-direction, there are 2p atomic orbitals in the z-direction and in the y-direction. Just the 2py orbitals on each atom are shown here.
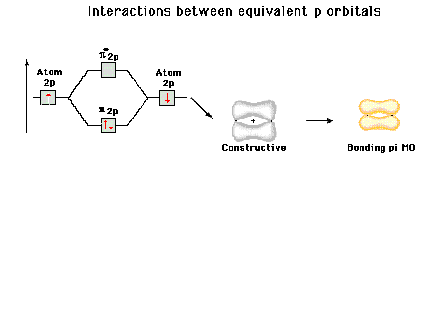
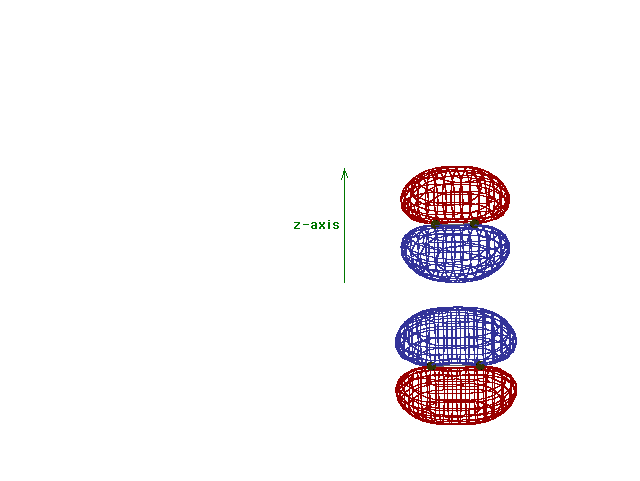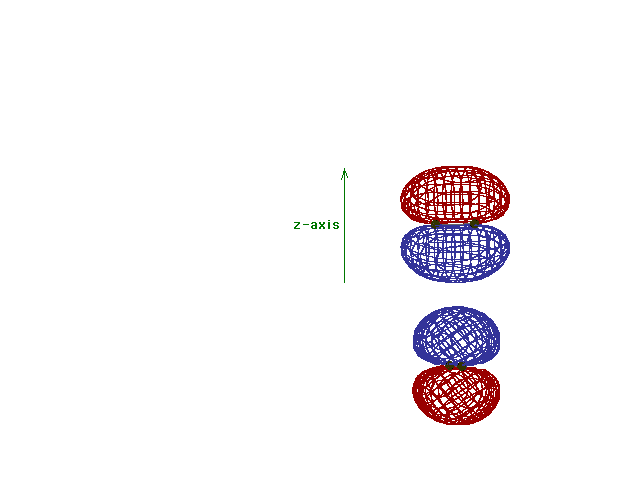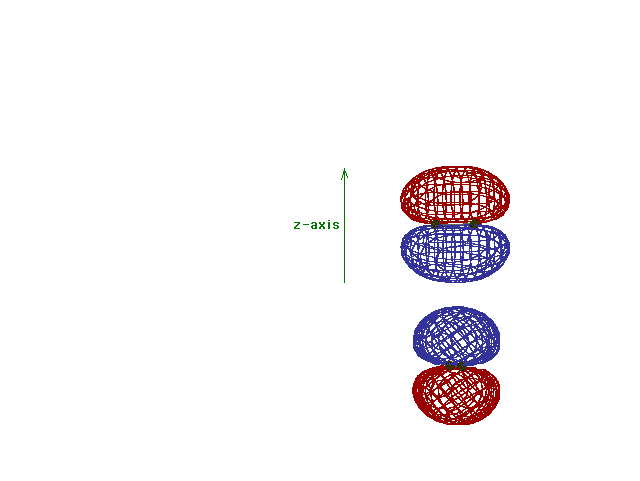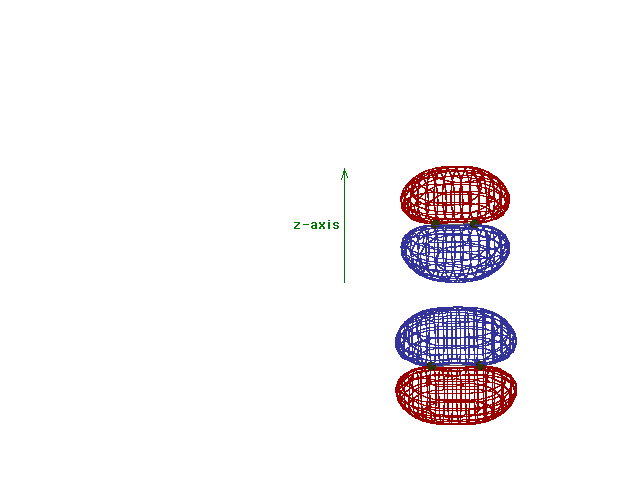
Energy diagram and geometry for the pi-2py (bonding) molecular orbital construction from the 2p atomic orbitals originally pointing in the y-direction, perpendicular to the bond axis and in the plane of the illustration. Constructive interference occurs in the region of overlap. (Recognize that there is an identical pi bonding level, same energy, constructed in the x-direction from the 2pz atomic orbitals.)
This is an animation of the computer-generated 2p bonding molecular orbital showing how the symmetry about the bond axis resembles that for the p-atomic orbital's symmetry about the nucleus. Hence the label.
Energy diagram and geometry for the pi*-2py (antibonding) molecular orbital construction from the 2p atomic orbitals originally pointing in the y-direction, perpendicular to the bond axis and in the plane of the illustration. Destructive interference occurs here, in contrast to what occurs for the bonding molecular orbital. (Recognize that there is an identical pi* antibonding level, same energy, constructed in the z-direction from the 2pz atomic orbitals.)
Re-defining how one calculates bond order within the context of molecular orbital theory.
The molecular orbital energy diagram for H2- and other isoelectronic species, all having bond order = 0.5. The electron configuration would be written as 1s2 *1s2 2s2
or, as in the current text, simply s2 *s2 s2.
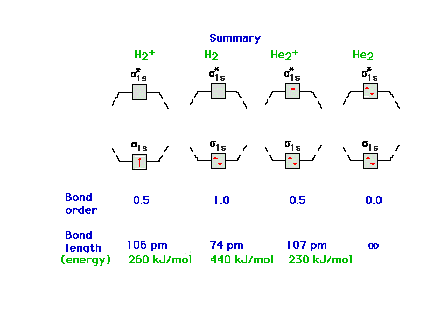
Molecular orbital energy diagrams for 1, 2, 3, and 4 electrons systems. The correspondence between bond order and bondlength and between bond order and bond energy is shown for each molecular species.
The molecular orbital energy diagram for Li2 containing all six electrons. Since antibonding electrons negate the effect of bonding electrons, the pair of * electrons cancels out the bonding characteristics of the pair of electrons and both pairs revert to the inner core 1s2 configurations that we expect from simpler considerations. The electron configuration could thus be written as [He][He]2s2.
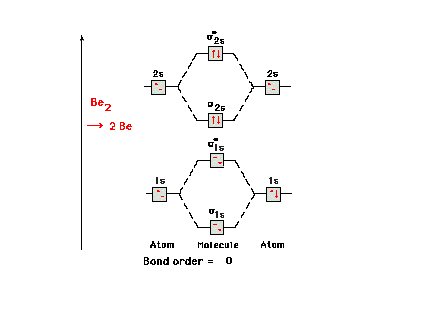
The molecular orbital energy diagram for Be2. Since the number of antibonding electrons is equal to the number of bonding electrons, there is no net bonding in this molecule and it simply breaks back up into two Be atoms.
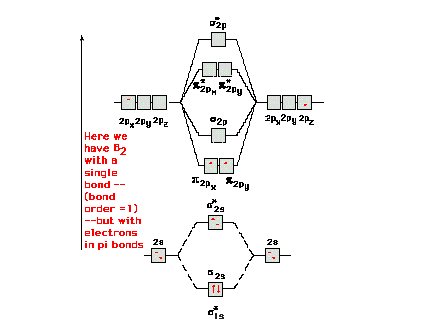
For "diboron", B2 we get a somewhat surprising result out of the molecular orbital energy diagram and the ensuing electron configuration. The ninth and tenth electrons go into the lowest energy available orbitals. These are the orbitals. There are two of equal energy and Hund's rule forces us to put one electron in each and with parallel spins. Thus we have bond order = 1, a single bond, but it is not a sigma bond. In fact, there is one electron in one pi-orbital and another electron in a second pi-orbital comprising this single bond.
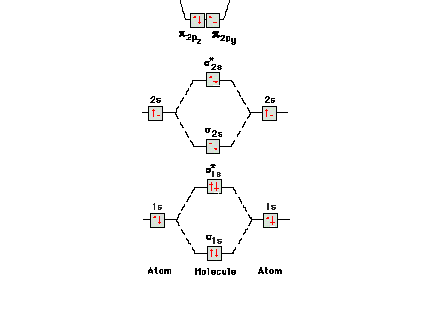
Molecular orbital energy diagram for the lower states in molecular nitrogen, N2. The lowest two molecular orbitals return to 1s, inner core electrons on each nitrogen atom. The next two pairs, with no net bonding effect, become lone pairs that can be pictured as being in 2s valence orbitals on each nitrogen.
The valence molecular orbitals in nitrogen that give rise to the triple bond, bond order = 3.



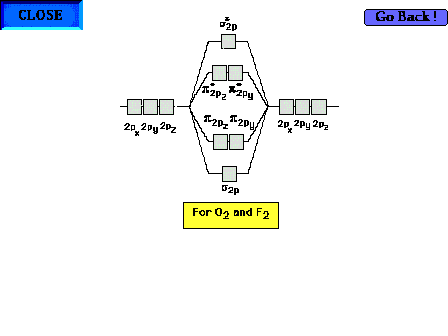
Click the Detour sign to see an optional explanation (several slides) of why the / sequence changes when O2 and F2 are reached. Note, you do not need to remember this reversal of sequence. For your convenience in 09-105, you can ignore it even if it seems to apply.
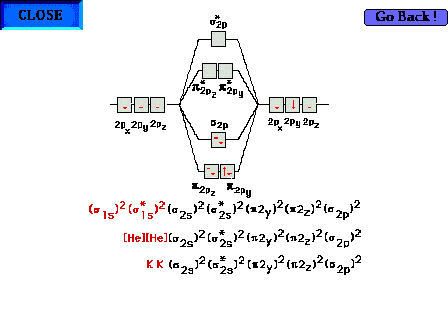
The electron configuration for all 14 electrons in N2. Three variations are shown on how to represent the inner core, 1s2 electrons on each nitrogen atom. Sometimes the two pi molecular orbitals are respresented with a single 4 symbol.
Comparison of ionization energies for atomic N and molecular N2 to illustrate that the bonding molecular orbital in the latter is more stable than the atomic orbital from which it "originates". That is, combining two N atoms leads to a more stable, bound nitrogen molecule, releasing energy.
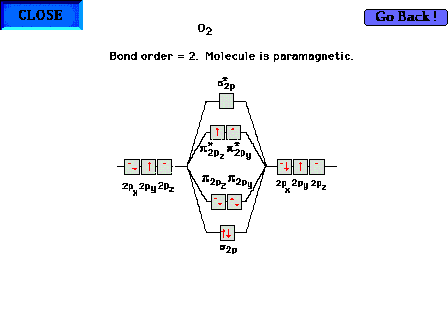
The highest occupied molecular orbitals in molecular oxygen. The bond order is 2, but is composed of a sigma bond and one net electron in each of the two orbitals. The molecule is paramagnetic due to the two parallel electron spins.
Comparison of ionization energies for atomic O and molecular O2 to illustrate that the antibonding molecular orbital in the latter is less stable than the atomic orbital from which it "originates". That is, electrons in the antibonding orbitals "want" to release energy by returning to atomic orbitals.