Now that we've discussed Prim's Algorithm, we are going to discuss a second
approach for solving the same problem. This approach is also a greedy
algorithm.
Although the implementation is a bit more complex, the basic algorithm is
very straight-forward. We simple attempt to add each edge from the original
graph to the minimum spanning tree, beginning with the lowest-weight edge and
finishing with the greatest-weight edge. We add the edge if it doesn't cause a
cycle and passs it up, if it does. We continue to add edges, until we've
added N-1 edges, where N is the number of verticies. Remember, spanning trees
have exactly N-1 edges -- never more, never less.
This works for more-or-less the same reason that Prim's Algorithm works. We
need to add n-1 edges to the graph. Adding the smallest n-1 legal edges to
the graph is guaranteed to give us the spanning tree with the least aggregate
weight. Since we don't add an edge if it creates a cycle, we know we'll have
a tree. Since we add exactly n-1 edges, we know that it will be a spanning
tree -- one less and it would be disjoint trees, one more and it would be
a more general graph with a cycle. And, since we add the smallest such edges,
we know it has the lowest total weight. And, it all works out, because it
is never the case that adding a more costly edge earlier would prevent
a cycle allowing the addition of super-cheap edges later.
In order to make it easy to select the candidates in the right order, from
the lowest weight to the highest weight, we store the edges in a
priority queue (heap). Then, selecting an edge is simply the
deleteMin() operation.
Another way of viewing the algorithm is to views the inital
configuration as a forrest of trees, with each vertex in its own, independent
tree. If we take this view, then adding an edge merges two trees into one.
When Kruskal's terminates, there is only one tree - the minimum spanning tree.
Let's take a look at the algorithm in operation, using the same graph as
we used last class:
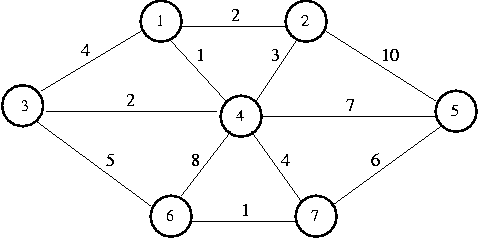
The following table shows the verticies sorted by weight and whetehr or not each vertex
was accepted. Remember, we evaluate each vertex, one-at-a-time, from the top of this list
down. In a real implemention, we would have added them to a heap, and be using deleteMin()
to get to the top one for each iteration.
| Edge
| Weight
| Action
|
| (1,4)
| 1
| Accepted
|
| (6,7)
| 1
| Accepted
|
| (1,2)
| 2
| Accepted
|
| (3,4)
| 2
| Accepted
|
| (2,4)
| 3
| Rejected
|
| (1,3)
| 4
| Rejected
|
| (4,7)
| 4
| Accepted
|
| (3,6)
| 5
| Rejected
|
| (5,7)
| 6
| Accepted
|
So, how can we figure out if adding a particular edge to a tree will create a
cycle? This is very important to Kruskal's Algorithm, because we only add an edge,
if doing so won't create a cycle.
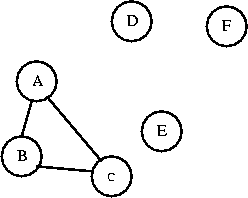
Imagine that each vertex in a graph is its own set (remember the
Set class you created for the lab?).
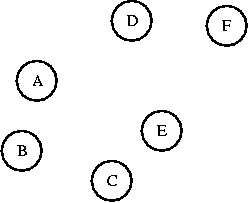
If you connect two vertices in the same set together, you'll create
a cycle. As long as you connect vertices from two different sets, you
won't create a cycle. A and B are in different sets. I'll connect them.
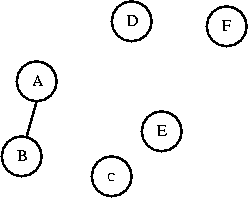
Now AB is a set. Can I connect C to AB? C and AB are in different sets,
I'll connect them. Now I have a set called ABC.
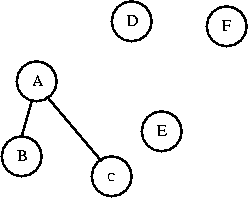
Can I connect C to B? C and B are in the same set, so connecting them
will create a cycle.
Earlier this semester, we created a Set class using LinkedLists. This class supported
a very broad array of Set operations. But, for this particular problem, we only
need to do two things: look in a set to see if an item is there (find) and
unite two sets (union). And, since the Set lab, we've learned about trees, which
added a powerful tool to our kit. Let's see how we can use trees to represent
sets in a way that leads to efficient Union and Find operations.
Again, imagine a graph, with each vertex as its own set. Now imagine that
each set of vertices is a tree. So before we connect any edges, each vertex
is its own tree, and the graph is a forest of trees.
We'll use an array to represent the trees. Create an array, with each
index of the array representing the corresponding vertex of the graph.
Place a sentinel value, -1, into each array element. We will use this
sentinel value to denote the root of the tree. Before we connect any edges,
each vertex is its own tree, so its the root. -1 represents the root of the
tree set.
0 1 2 3 4 5 6 7
[-1] [-1] [-1] [-1] [-1] [-1] [-1] [-1]
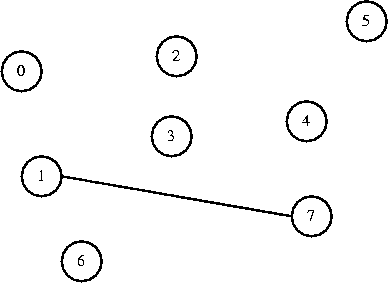
Now I decide to connect 7 to 1. They are in different sets, so I connect them.
0 1 2 3 4 5 6 7
[-1] [-1] [-1] [-1] [-1] [-1] [-1] [ 1]
The parent of 7 is now 1, and 7 is no longer the root of the tree. If we
want to find 7's parent, we simply look at its value, which is 1. To find
1's parent, we look at its value, which is -1, indicating that 1 has no
parent and is the root of the tree.
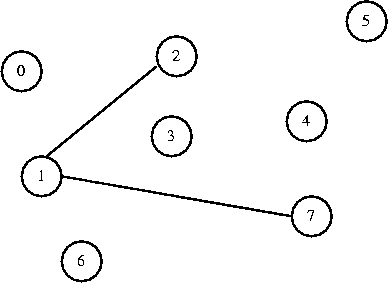
Now I decide to connect 2 to 1. They are in different sets, so I connect them.
0 1 2 3 4 5 6 7
[-1] [-1] [ 1] [-1] [-1] [-1] [-1] [ 1]
Now I decide to connect 0 to 7. They are in different sets, so I connect them.
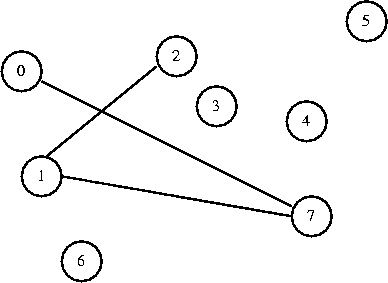
0 1 2 3 4 5 6 7
[ 7] [-1] [ 1] [-1] [-1] [-1] [-1] [ 1]
I want to connect 4 to 6. They are in different sets, so I connect them.
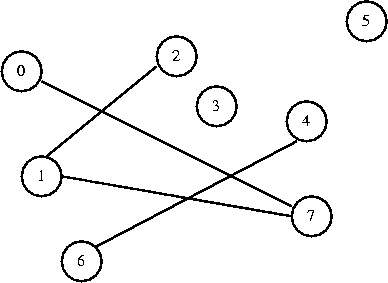
0 1 2 3 4 5 6 7
[ 7] [-1] [ 1] [-1] [ 6] [-1] [-1] [ 1]
I want to connect 5 to 6. They are in different sets, so I connect them.
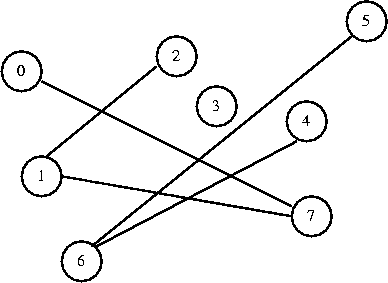
0 1 2 3 4 5 6 7
[ 7] [-1] [ 1] [-1] [ 6] [ 6] [-1] [ 1]
Note that connect 4 to 5 would now create a cycle.
I want to connect 1 to 4. They are in different sets, so I connect them.
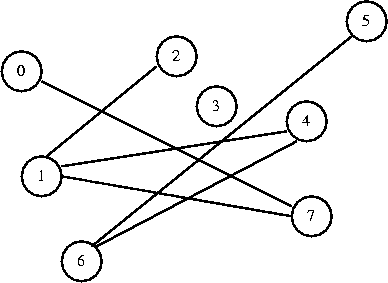
0 1 2 3 4 5 6 7
[ 7] [ 4] [ 1] [-1] [ 6] [ 6] [-1] [ 1]
How do you find out what set a particular vertex of the graph belongs to?
You simply follow its ancestors up until you find an array element with a
value of -1. At this point, all vertices except 3 are in the same set
-- 6. 6 is the only element with a value of -1. Vertex 6 is the root of
the tree consisting of all of the vertices in the graph.
The operation that connects to vertices by changing the array element
value of one to be the other is called union. The operation that
finds the root of a particular vertex's tree is called find.











