Vibration #3: The Human Vocal Chords
Introduction:
“The larynx is
located in the throat and contains the vocal chords and glottis. With
the exhalation of breath, the diaphragm forces air up through cartilage
"horn" of the larynx by contracting. The air moves through the vocal
chords, which are situated in the muscular vibrating folds of the
larynx, and the glottis, the space formed between them. By stretching
the vocal chords, adjusting the tension and varying the air pressure
through the glottis, the pitch of our voice is adjusting, tuning higher
or lower. A lower sound requires a longer column of air and is felt in
the chest, a higher sound uses a shorter column of air and is felt in
the nose and head.” (http://md.essortment.com/vocalchordanat_rzii.htm)
In this example you
will execute modal analysis of the vocal chords and find their natural
frequency for a person with these given anatomical dimensions.
Physical Problem:
The chords are free
to vibrate within the two flaps when air rushes past them, however, they
are firmly attached to the larynx on the circumference of the circle.
Problem Description:
·
The
chords have dimensions and orientation as shown in the figure.
·
They
are approximately 2mm thick.
Assume the
circumference of the vocal chords are connected to the larynx and are
completely fixed in all degrees of freedom. The chord material is
assumed to be solid and material properties are constant and isotropic.
·
Young’s Modulus = 6.7e7
·
Poisson’s Ratio = 0.1
·
Density = 898
·
Objective:
To
determine the natural frequencies of vibration
To
generate animations of these vibrations.
Figure:
The cylinder that
defines the membrane that forms the vocal chords is 2 mm thick. It has
a radius of 0.025 m.
The triangular
prism that defines the air column in the center of the vocal chords is
positioned at (0, -0.025), has a radius of 0.048 m, set at an angle of
90° and has a depth of 0.015m.


mesh size of
0.002
IMPORTANT:
Convert all
dimensions and forces into SI units.
·
Create the cylindrical solid defining the basic shape of
the vocal chords.
·
Create the triangular prism that defines the air channel
between the vocal chords.
·
Subtract this volume from the cylinder you first created
such that the final vocal chord shape remains.
·
Define the Material Properties of the vocal chords. (Hint:
The Elastic Modulus, Poison’s Ratio and the density of the vocal chords
is important to define)
·
Define the Element Properties as a Tet 10 node 92
Structural Solid.
·
Mesh the vocal chords. (Do so by setting the global size
of the elements to 0.002.)
·
Apply the boundary conditions. (Displacement of zero on
all the outer areas of the vocal chords. These are the areas that would
technically be connected to your throat. )
·
Solve for the natural frequencies of vibration of the
vocal chords. (Use a modal analysis using the Block Lanczos Mode
Extraction method and solve for 5 modes.)
·
List the nodal frequencies of vibration for the vocal
chords.
·
From the results obtained, read the first set, then
animate the mode shape using 60 frames with a 0.03 second time delay
between frames. Be sure to show the DOF Solution with both the Deformed
and Undeformed Edge. This will properly demonstrate the vibration
patterns in the vocal chords.
·
Plot the nodal solutions to use as screenshots and compare
with the answers below.
(These are the
results you should expect: *Note: Your results may be slightly
different due to “mesh uniqueness” but this difference should only be
VERY small.)
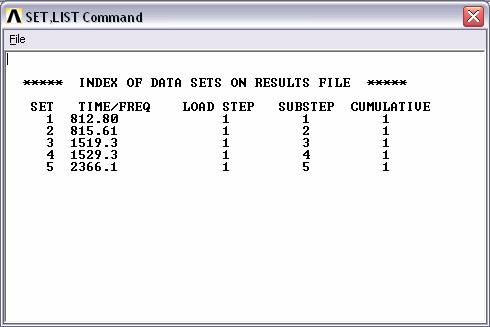
(Modes of
vibration:)
First

Second

Third

Fourth

Fifth
