Lecture #19
Text: Starting Chapter 14 at Section 2
  CURMUDGEON GENERAL'S WARNING. These "slides" represent highlights from lecture and are neither complete nor meant to replace lecture. It is advised not to use these as a reliable means to replace missed lecture material. Do so at risk to healthy academic performance in 09-105.
Lecture Outline Quantum Theory of the Chemical Bond

Molecular orbitals (in "homonuclear diatomic molecules"

Approximated by combinations of atomic orbitals

Constructive and destructive interference effects

Combining 1s atomic orbitals to get molecular orbitals

"Sigma" bonding molecular orbital

"Sigma" antibonding molecular orbital

Combining 2p atomic orbitals

"Sigma" bonding molecular orbital
Recall all that you've learned about wave functions and atomic orbitals, because we now start the adventure with electron behavior in molecular systems and develop the modern theory of the chemical bond.
Solving the Schrodinger wave equation for a system in which there is more than one center of force (a single nucleus) is difficult. Just a few years ago, John Pople, retired Professor of Chemistry at Carnegie Mellon, shared the 1998 Nobel Prize in Chemistry for devising mathematical tools amenable to computation that have greatly eased the problem if one resorts to using a computer. Approximate wave functions can be assembled using the ones we're already intimately familiar with: the hydrogen-like, one-electron atomic orbitals.
Among the unusual properties associated with the mathematics of waves is that of "interference". This occurs even for classical waves such as water waves and sound waves. Depending on whether combining waves have the same sign of their amplitudes or opposite signs, (i.e. they are in phase or out of phase,) the waves interfere constructively or destructively, respectively. As usual, we will visualize the complicated multidimensional appearance of the wave amplitudes by contour outlines in 2-D.
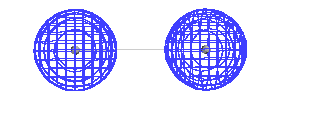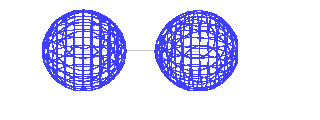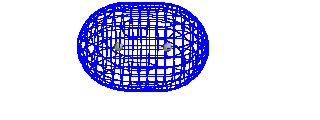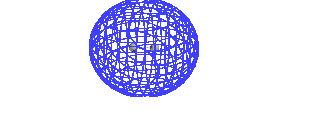
If we add together a 1s atomic orbital on one hydrogen atom with an identical 1s atomic orbital centered on another nucleus, the resulting orbital (whether there are electrons there or not) closely resembles the more exact orbital one would calculate by highly sophisticated mathematical techniques.Recalling the significance of an orbital, this would then indicate where an electron would be expected to be found if we placed an electron in the system. It would also be used to calculate the energy such an electron would have. Energy and geometry are our recurring themes, n'est pas?
This is a calculated solution for the constructive interference result.
An electron in an orbital about two protons has a potential energy indicated by the heavy curve if constructive interference of the atomic orbitals represents the electron's orbital. There is a certain proton-proton distance at which the energy is minimum. This is close to the bond length in the system with one electron.  
If destructive interference represents the orbital in which the electron happens to be found, the linear combination results in a depeletion of electron density between the positively charged protons. They repel each other under these circumstances.  
If destructive interference represents the orbital in which the electron happens to be found, the linear combination results in a depeletion of electron density between the positively charged protons. They repel each other under these circumstances.  
This is the destructive interference combination of 1s atomic orbitals
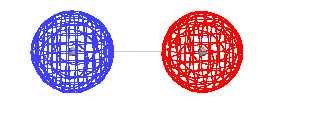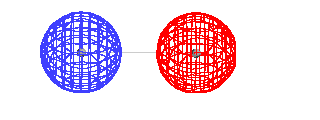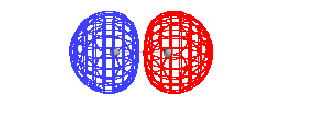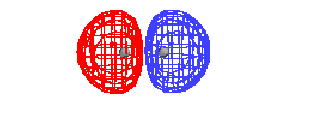The total energy of the ground state of H2+ as a function of the distance between the protons.
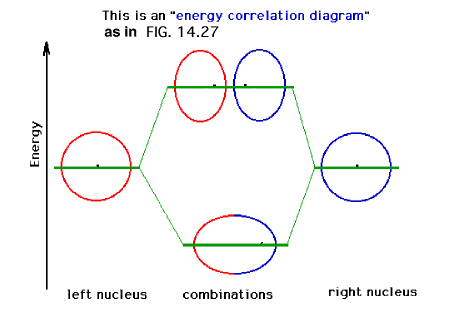
A schematic of the orbitals on separated protons relative to "close" protons. The constructive combination of atomic orbitals gives rise to a system lower in energy than the isolated system and is a bonding molecular orbital.  
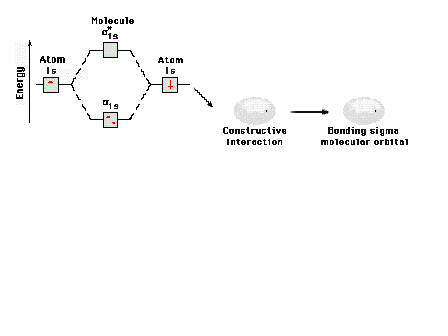
Energy diagram and geometry for the -1s (bonding) orbital construction.
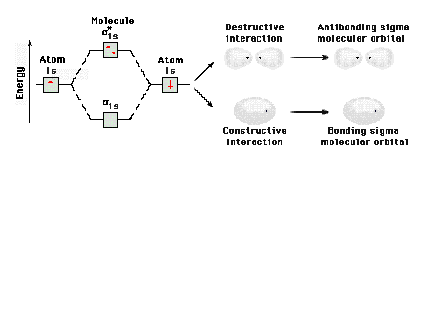
Energy diagram and geometry for the *-1s (antibonding) orbital construction
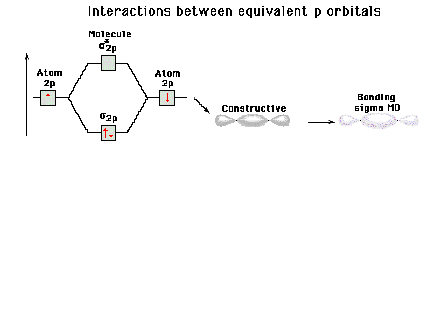
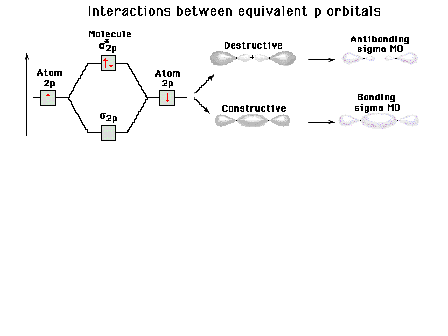
Energy diagram and geometry for the sigma-2px (bonding) orbital construction from the 2p atomic orbitals originally directed along the bonding (x) axis.
This (with luck) is an animation of the computer-generated 2p (or p) bonding molecular orbital showing how the symmetry about the bond axis resembles that for the s-atomic orbital's symmetry about the nucleus. Hence the label.
Energy diagram and geometry for the *-2p (antibonding) molecular orbital construction
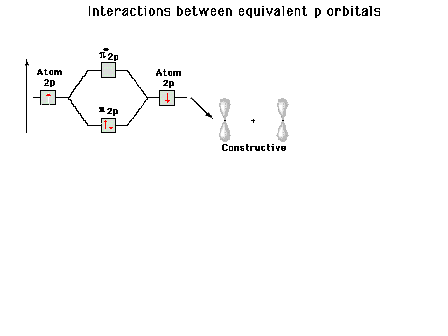
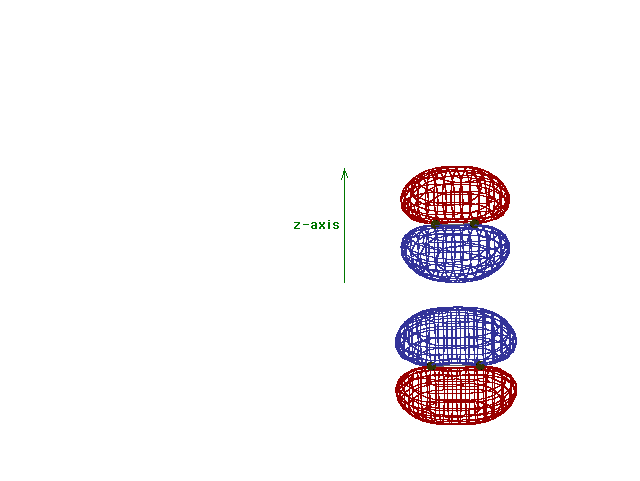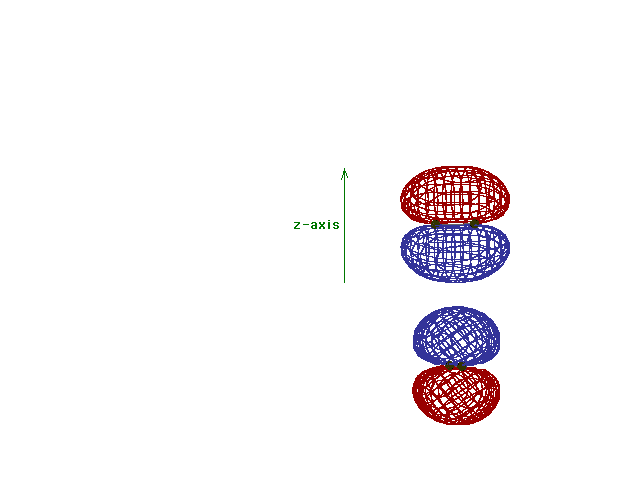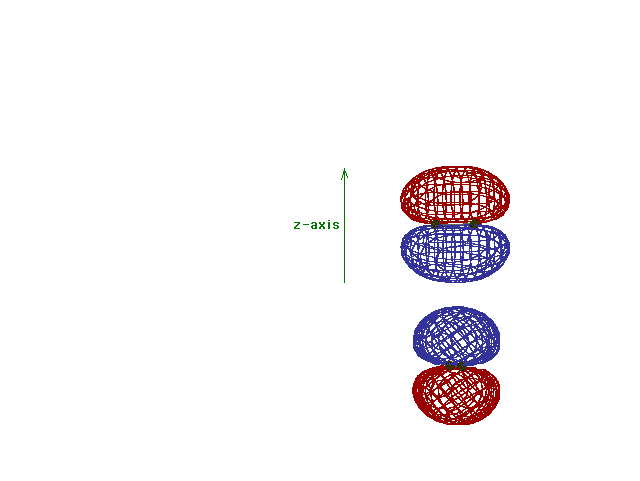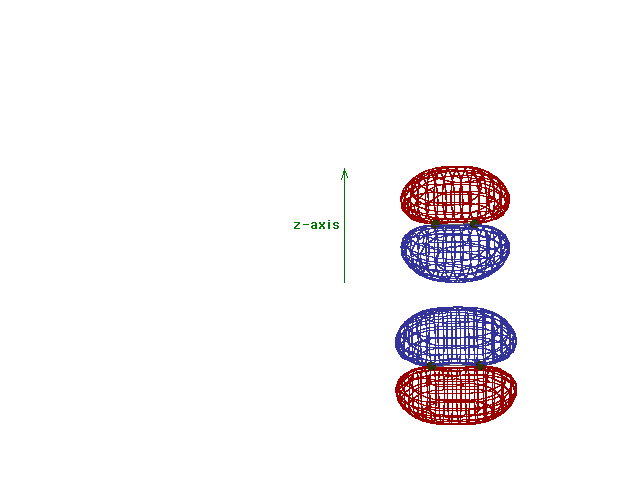
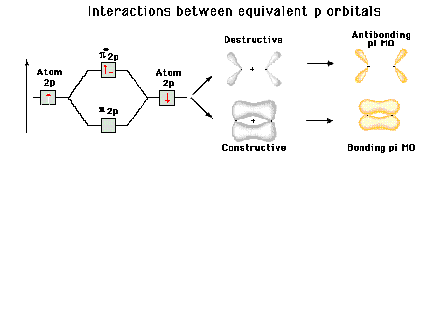
A reminder that, perpendicular to the bond axis in the x-direction, there are 2p atomic orbitals in the z-direction and in the y-direction. Just the 2py orbitals on each atom are shown here.
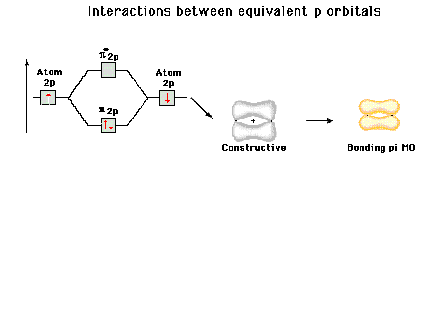
Energy diagram and geometry for the -2py (bonding) molecular orbital construction from the 2p atomic orbitals originally pointing in the y-direction, perpendicular to the bond axis and in the plane of the illustration. Constructive interference occurs in the region of overlap. (Recognize that there is an identical pi bonding level, same energy, constructed in the x-direction from the 2pz atomic orbitals.)
This is an animation of the computer-generated 2p bonding molecular orbital showing how the symmetry about the bond axis resembles that for the p-atomic orbital's symmetry about the nucleus. Hence the label.
Energy diagram and geometry for the *-2py (antibonding) molecular orbital construction from the 2p atomic orbitals originally pointing in the y-direction, perpendicular to the bond axis and in the plane of the illustration. Destructive interference occurs here, in contrast to what occurs for the bonding molecular orbital. (Recognize that there is an identical * antibonding level, same energy, constructed in the z-direction from the 2pz atomic orbitals.)