Calculate Gains

You will choose three values of gain for this controller to demonstrate different response types, overdamped, critically damped, and underdamped. You will choose the gains to meet settling time and/or percent overshoot overshoot requirements. You will use MATLAB (in the room next-door) to make the calculations. You will then calculate the appropriate resistor values to give you the appropriate gains. For this section you may find the MATLAB tutorials to be helpful. Refer to www.me.cmu.edu/matlab/html and go to the Root Locus tutorial. The Motor Speed Example is useful too.

  1. Generate Root Locus in MATLAB
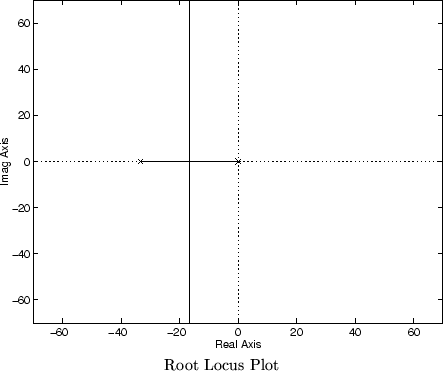
    The root locus is a plot of all possible closed-loop pole locations as the gain, Ki is varied. You can use this plot to select gains.
    Define the variables num and den to be the numerator and denominator polynomials of the open-loop transfer function, including the 1/s in the controller (but not Ki).
    Type rlocus(num,den). The root locus, similar to that shown below will be drawn. Print it out.

    figure106

  2. Find Pole Locations
    Caculate the pole locations which give you the following three responses. The desired poles must lie on the root locus since these are the only possible pole locations given the controller you are implementing. Do not calculate the gains yet - you will do this later. Just determine where on the root locus the appropriate pole(s) will lie.
    Overdamped, Ts=0.4s.
    When the system is overdamped, even though the system is second order, one pole is much ``faster'' (i.e. further to the left) than the other. We can approximate the system as a first order system with a single pole (the slower pole). Choose this pole to give the appropriate 98% settling time.
    Critically Damped
    The critically damped system will have as fast a Ts as possible while maintaining no overshoot. The damping ratio of the second order system will be 1, and there will be two equal real roots.
    Underdamped, %OS=25%.
    In the underdamped system, you will have two complex-conjugate poles and a damping ratio of less than 1. It turns out that in this system, Ts does not change from the critically damped Ts. Determine the damping ratio to a achieve 25% overshoot and the corresponding poles
  3. Find Gains in MATLAB
    For each of the pole locations you computed, compute the required Ki.
    With the root locus plot on the screen, type [K,poles]=rlocfind(num,den) at the command prompt.
    Click with the mouse on the root locus plot at the desired pole location.
    Matlab will return the pole location you selected and the corresponding gain, Ki. If you did not get quite the poles you were looking for, try again.
  4. Calculate Potentiometer Values.
    For each value of gain, Ki, calculate the corresponding value for the potentiometer, R3. Be sure to take into account both op-amp circuits in you calculation.

    Ajay Juneja
    Tue Apr 20 13:30:59 EST 1999

    Next-Closed Loop Response

[ Up ] [ Plant Identification ] [ Controller Circuit ] [ Calculate Gains ] [ Closed Loop Response ] [ Writeup ]