Junkai Huang - 16-726 Learning-based Image Synthesis

Background

This project explores gradient-domain processing, a simple technique with a broad set of applications including blending, tone-mapping, and non-photorealistic rendering. The primary goal of this project is to seamlessly blend an object or texture from a source image into a target image. The simplest method would be to just copy and paste the pixels from one image directly into the other. Unfortunately, this will create very noticeable seams, even if the backgrounds are well-matched. How can we get rid of these seams without doing too much perceptual damage to the source region? Here we take the following approach: The insight we will use is that people often care much more about the gradient of an image than the overall intensity. So we can set up the problem as finding values for the target pixels that maximally preserve the gradient of the source region without changing any of the background pixels. Note that we are making a deliberate decision here to ignore the overall intensity! So a green hat could turn red, but it will still look like a hat.

Toy Problem

In this toy problem, we reconstruct an image v from a source image s using the identical-xy-gradient constriants. We denote the intensity of the source image at (x, y) as s(x,y) and the values of the image to solve for as v(x,y). So we have the following 3 objectives to minimize:

1. Minimize ((v(x+1,y)-v(x,y)) - (s(x+1,y)-s(x,y)))**2, so the x-gradients of v should closely match the x-gradients of s.
2. Minimize ((v(x,y+1)-v(x,y)) - (s(x,y+1)-s(x,y)))**2, so the x-gradients of v should closely match the y-gradients of s.
3. Minimize (v(1,1)-s(1,1))**2 so that the top left corners of the two images should be the same color.

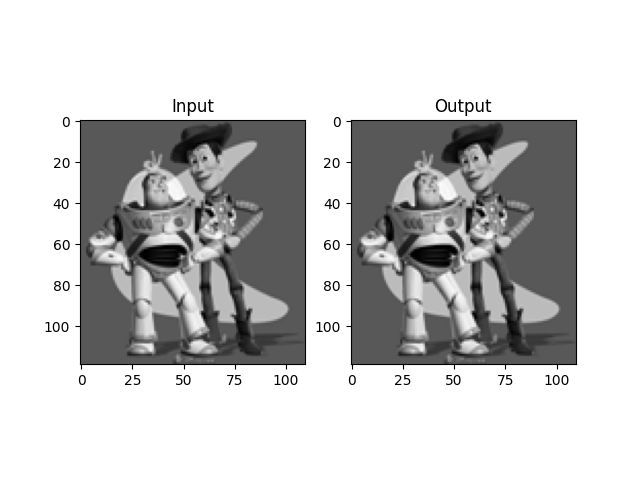
Poisson Blending

Given a source image s and target image t, we first select the boundaries of a region in s and specify a location in t where it should be blended. Then, transform (translate) s so that indices of pixels in the source and target regions correspond. Ideally, the background of the object in the source region and the surrounding area of the target region will be of similar color. To achieve this, we solve the blending constraints:

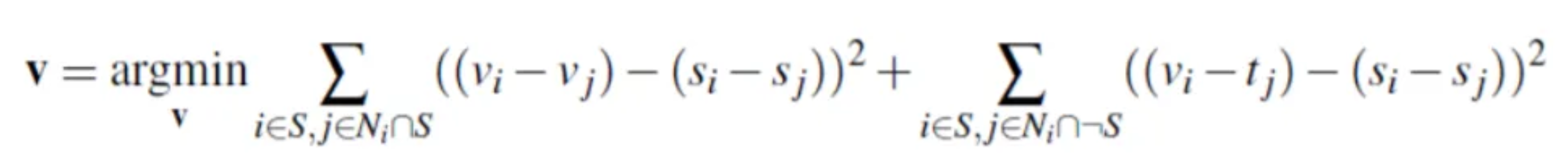
Here are the results we have:

Result 1 - My Favorite

Transfer Mike Tyson's face tattoo to Conor McGregor's face. Poisson blending is doing well on this task as it blends Tyson's tattoos into Conor's face so perfectly that we basically can't see the seams. By the way both of them are my favorite Boxing/MMA atheletes.

Result 2 - Good

Transfer a penguin to the CMU campus on a snowy day. The result is good and we can barely see any artifacts.

Result 3 - Not that good

Transfer a polar bear into a forest. This time the result is not good as we can see the conspicuous blurry artifacts around the transfered bear. That's because the background of the polar bear source image contains only low frequency information (snow, ocean, sky) where the gradients are small, but the target image consists of high frequency info like woods, leaves and grass where the gradients are large and change frequently. Such constrast in gradients makes it very difficult to blend the source image into the target image using gradient-domain fusion.

Result 4 - Not that good

Transfer a polar fox to a desert. Another typical failure case due to the drastical background gradient difference between the source and target image.

Extra: Mixed Gradients

In the previous results we already find that the large background gradient difference can lead to conspicuous artifacts in the poisson blending results. To address this issue, for each pixel in the blended image, we can lt it follow either the gradient of the source image or the gradient of the target image, whichever has a larger absolute value. Here are the results:

Extra: Color2Gray

When directly converting RGB image to grayscale image, some perceptual feature may be lost. For example when after converting a color blind testing card to grayscale in a naive way, we cannot see the number anymore. But we can incorporate gradient processing to RGB2GRAY conversion in order to preserve such kind of perceptual feature. Specifically, we first convert the image from RGB space to HSV space. We use Saturation (S) channel as the source image, and Value (V) channel as the target image to optimize the following objective:

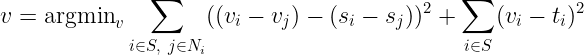
So that within the masked area, the result image will have similar gradient to the S channel, and similar intensity to the V channel. Here are the results: