Assigment 4

1. Sphere Tracing

def sphere_tracing(self, implicit_fn,
    origins, # Nx3
    directions, # Nx3
):
    N_rays = origins.shape[0]
    device = origins.device
    near, far = self.near, self.far
    eps = 1e-5
    t = torch.ones(N_rays, 1, device=device)*near
    mask = torch.zeros(N_rays, 1, dtype=torch.bool, device=device)
    while True:
        points = origins + t * directions
        dists = implicit_fn.sdf(points)
        curr_mask = dists < eps
        mask = torch.logical_or(mask, curr_mask)
        dists[mask] = 0
        t = t + dists
        idx = torch.logical_not(mask)
        t_left = t[idx]
        if torch.all(t_left >= far):
            break
    return points, mask

Explanation: We employ the sphere tracing (p = o + t*d) equation to move, and maintain a mask of intersections that gets updated in every iterations (m = m | m_it). We only move on points which have not been interesected yet (by setting d[m] = 0). The loop breaks when all the non-intersected points are beyond the “far” distance.

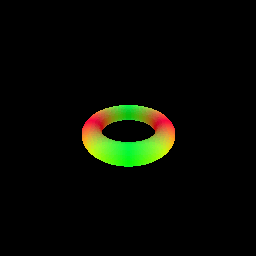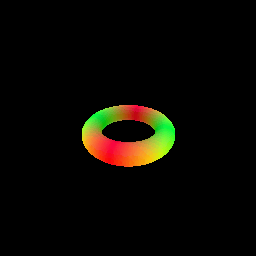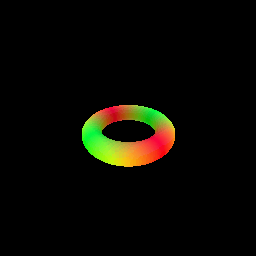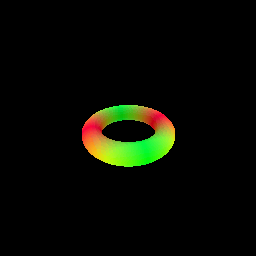
2. Optimizing a Neural SDF

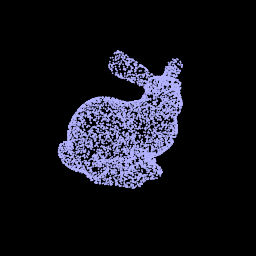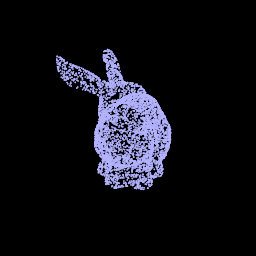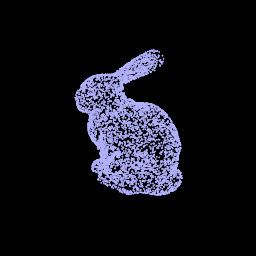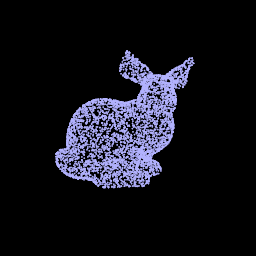
3. VolSDF

Method	Epoch = 50	Epoch = 150	Epoch = 250
VolSDF
VolSDF-Geometry

An intuitive explanation of what the parameters alpha and beta are doing:

The outside and inside of the surface is defined by 0 and alpha, and the parameter 1/beta controls the sharpness of the drop from inside to outside. The maximum density inside the surface is bounded by the parameter alpha.

Q1. How does high beta bias your learned SDF? What about low beta?

A1. A low beta would imply that density would tend to zero, that is, converge to a scaled indicator function. The learned SDF would approximate a scaled indicator function with low beta. A high beta would reduce the opacity of the surface.

Q2. Would an SDF be easier to train with volume rendering and low beta or high beta? Why?

A2. I experimented by training with betas = [ 0.0005, 0.05, 0.5 ]. I observed experimentally that lower beta is easier to train as it converged to much better looking surfaces. That is possibly because the expected surface better approximates a scaled indicator function and with the appropriate sampling procedure, it’s easier to learn the color and the geometry. Beta=5 didn’t converge to a shape that looked like a construction vehicle at all. We see the outputs after first 50 epochs below.

Q3. Would you be more likely to learn an accurate surface with high beta or low beta? Why?

A3. It depends on the kind of object we are trying to model, for instance, surfaces with higher permeability would be better learnt with a higher beta than a lower beta than vice versa.

However, it does appear that the paper “Volume Rendering of Neural Implicit Surfaces” indicates that we would be more likely to learn a better bound on opacity error with higher beta. This has been shown in the paper in Lemma 2. The error is bound by epsilon, and beta is inversely proportional to epsilon (see Eq 16).

4. Neural Surface Extras

4.2 Fewer Training Views

Method	Epoch = 50	Epoch = 150	Epoch = 250
VolSDF
VolSDF-Geometry
NERF

4.3 Alternate SDF to Density Conversions

Method	Epoch = 50	Epoch = 150	Epoch = 250
NeUS
NeUS-Geometry