Project 2 - Poisson Blending

Source Image

Target Image

Poisson Blending
Copy and pasting a source image onto a target image is a fundamental way to manipulate and generate content. A naive way of copy and pasting source onto another target image is simply by overwritting the rgb values of the target image. However, this can lead to very visible artifacts, such as an abrupt edges and mismatching background colors. We want to blend the images together in a way that minimizes visual dissonance and artifacts. It has been shown that edges, i.e. image gradients, play an important role is expressing texture and the clashes of texture leads to abrupt artifacts. Therefore, Poisson blending by Perez et al. aims to minimize artifacts by minimizing the error between the gradients of the final image and the gradients of the source image in the masked region while matching the intensity of the target image outside of the masked region. This website will show the outputs of the toy example, poisson blending, and mixed gradient poisson blending.
Toy Example
In the toy example, we are trying to reconstruct the input image by solving a least squares optimization problem on three specified objective functions: the error between x gradients, the error between y gradients, and the intensity of top left pixel. By minimizing these objective functions, we effectively reconstruct the image. Since there is no noise involved, we can arrive at an optimal solution which reconstructs the input image with no error. We construct the objective functions in the form of $Ax=b$ where $A$ is (num_pixel*2+1, num_pixel) matrix representing the objectives at each pixel, and $b$ is (num_pixel*2+1, 1) also used to represent the objectives. Lastly, $x$ (num_pixel, 1) is the final image that minimizes the objectives.
Figure. Toy example input and output.
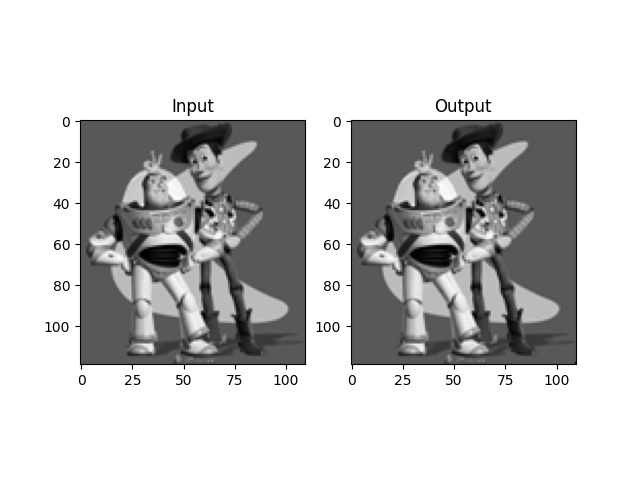
Toy Example
Poisson Blending
We setup Poisson blending as an optimization problem on sparse matrix A with gradient objective functions similar to the toy example. Here, we have $A$ of size (num_pixels*4, num_pixels) and $b$ of size (num_pixels*4, 1) representing the x and y gradients at each pixel. For regions inside the mask, we want to match the gradient of the final output to the gradient of the source, for pixels outside the mask we simply want the final output to equal the pixel intensity at the target image. We perform this optimization independently over the three color channels and combine the final output. The optimization tries to preserve the features, edges, from the source so it is still recognizable in the final image and tries to blend the colors in the target in a similar gradient to the gradients in the source.
The equation we are optimizing can be found on the assigment website. $v$ is the final output, $s$ is source image, $t$ is target image. $i$ represents a single pixel, $j$ represents the four neighbor pixels. $$\newcommand{\argmin}{arg min} \boldsymbol{v} = \argmin_{\boldsymbol{v}}\sum_{i \in S, j \in N_i \cap S}((v_i - v_j) - (s_i - s_j))^2 + \sum_{i\in S, j \in N_i \cap \neg S}((v_i - t_j) - (s_i - s_j))^2.$$
Figure. Below are visualizations of the swimming bear. We see that the poisson blending fixes the sharp edge artifacts but shifts the color of the source a bit to blend with the target.

Source

Mask

Target

Naive Overlay

Poisson Blending
Figure. Below are visualizations of the legendary professor Jun-Yan Zhu. We see that poisson blending blends the source so the color is similar to target while preserving gradients of the source so we can still recognize the legendary professor. This example works well.

Source

Mask

Target

Naive Overlay

Poisson Blending
Figure. Below are visualizations of the best TA Sheng-yu Wang. Since the source color is similar to target color, we see that colors of the target and blended together with edges from the source nicely. This example works well.

Source

Mask

Target

Naive Overlay

Poisson Blending
Figure. Below are visualizations of the best TA Sheng-yu Wang. This example works poorly. This is because source color and target color are wildly different. While trying to preserve the gradients of the source, the color shifts to the blue tone and the low contrast makes in harder to see the best TA.

Source

Mask

Target

Naive Overlay

Poisson Blending
Mixed Gradients
While Poisson blending works well, we see that in areas where the source is a constant color, the output image has a blur since it tries to match the 0 gradient of the source. This is shown in the helicopter example and also the stickfigure example below. In this case, we can mix the gradients such that we want the output image's gradients to match the highest gradient from either the source or the target. This helps to preserve the more noticeable features while ignoring 0 gradient regions where the content there is less important.
Figure. Below are visualizations of helicopter. Notice how with Poisson blending the area around the helicopter has a blur to it. When we use mixed gradient Poisson blending, we see that the region near the helicopter are close to the target, making the scene more realistic as it only fits to the highest gradient.

Source

Mask

Target

Naive Overlay

Poisson Blending

Mixed Poisson Blending
Figure. Below are visualizations of stickman. We see that mixed gradients help to copy the high value gradients which identify edges of text or drawings and drastically improves the realistic look when blending a source with clean background onto a target with texture.

Source

Mask

Target

Naive Overlay

Poisson Blending

Mixed Poisson Blending