Assignment #2 - Gradient Domain Fusion

Background

Sometimes we want to combine the object from one image to the background of another. Due to the difference in color tone and light between images and the unperfect crop, direct copy-and-paste always results in unsatisfactory outcomes.

Motivation

Fuse two images as seamless as possible.

Toy Problem

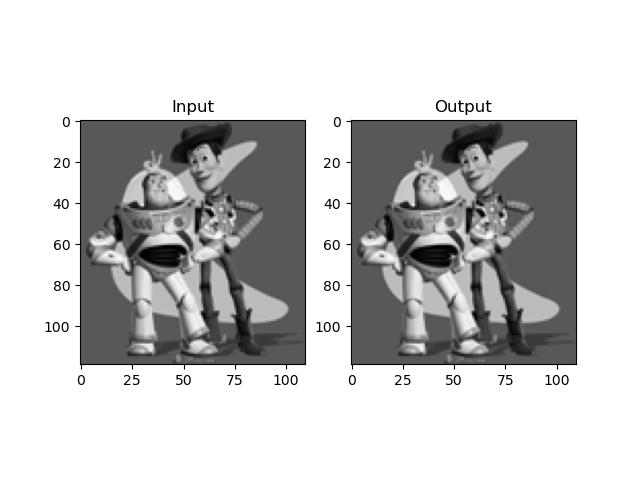
This problem requires a basic implementation of calculating (discrete) gradients and forming the least square error constraints in a matrix $(\mathbf{A}v-\mathbf{b}{)}^2=0$$({\bf A}v-{\bf b})^2=0$.

We want to reconstruct an image with only the up-left corner pixel information. Although there is no other direct intensity of other pixels, we can use a 2-direction gradient to simulate the original image and get a similar result $v$$v$.

Here are three objective functions:

1. $\mathrm{argmin}((v(x+1,y)-v(x,y))-(s(x+1,y)-s(x,y)){)}^2$$\operatorname{argmin}((v(x+1, y)-v(x,y)) - (s(x+1, y)-s(x,y)))^2$ -- in the same pixel line, reconstructed gradient(right - left) should be close to the source image.
2. $\mathrm{argmin}((v(x,y+1)-v(x,y))-(s(x,y+1)-s(x,y)){)}^2$$\operatorname{argmin}((v(x, y+1)-v(x,y)) - (s(x, y+1)-s(x,y)))^2$ -- in the same pixel column, reconstructed gradient(down - up) should be close to the source image.
3. $\mathrm{argmin}(v(0,0)-s(0,0){)}^2$$\operatorname{argmin}(v(0,0)-s(0,0))^2$ -- copy the pixel on the top-left corner of the source image and paste it to the reconstructed $v$$v$.

Once the numbers in parameter matrix $A$$A$ and the bias matrix $b$$b$ are set, np.linalg.lstsq can solve the appropriate $v$$v$. The result is shown as follows.

Poisson Blending

The blending constraint is

Similar to the toy problem, it turns to 2 objectives.

1. $\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}{\mathrm{n}}_{\mathrm{v}}\sum _{i\in S,j\in N_i\cap S}((v_i-v_j)-(s_i-s_j){)}^2$$\operatorname{argmin_v} \sum_{i\in S, j\in N_i \cap S}((v_i - v_j)-(s_i-s_j))^2$
2. $\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}{\mathrm{n}}_{\mathrm{v}}\sum _{i\in S,j\in N_i\cap \mathrm{\neg }S}((v_i-t_j)-(s_i-s_j){)}^2$$\operatorname{argmin_v} \sum_{i\in S, j\in N_i \cap \lnot S}((v_i-t_j)-(s_i-s_j))^2$

Also, background of the target image should be directly copied to the reconstructed one, which can be written as the third objective in the format below, but actually there is no need to put this constraint into the matrix solving process:

3. $\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}{\mathrm{n}}_{\mathrm{v}}\sum _{i\in \mathrm{\neg }S}((v_i-t_i){)}^2$$\operatorname{argmin_v} \sum_{i\in \lnot S}((v_i-t_i))^2$

In the code implementation, I use 1 and 2 constraints on two separate groups of pixels. The partition depends on whether the 4 adjacent pixels of the specified center is inside the masked region. Notice that if a pixel on the border of mask has 2 adjacent pixels outside the mask, then only these two gradients should use constraint 2, but the other two still use constraint 1.

For saving the computational cost, i.e. simplify the linear matrix solving by reducing variable dimension, I first crop the bg, fg, and mask by bounding box of the masked region, and send those cropped small patches to fuse. This will not effect the output because bg's pixel intensity is fixed.

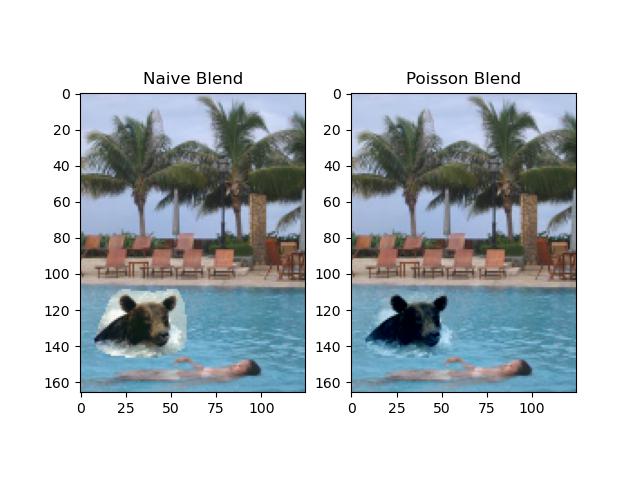
Here is the result of the given sample. Result from Posisson Blend is smoother than the naive copy-and-paste.

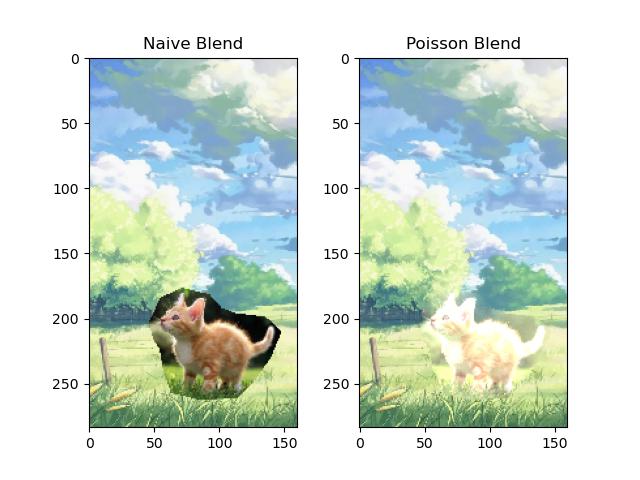
Then I tried several custom examples. I slightly modified the masking_code(many thanks to the author) to ensure the source is resized to fit the target size.

In the first try, I use a real kitty image as source and an anime background as target. The Poisson Blend(PB) result is still better than Naive Blend(NB, and the kitty is really cute), but there's artifacts that make the PB result unperfect. Since this anime target tend to use bright color (~(255, 255, 255)), there's not enough space for the cropped kitty to adjust its gradient given the fixed border of the target image. Also, the dark background left in the cropped source makes the kitty turn even brighter, leading to a result like over-exposure. Moreover, the texture of BG in the cropped source is not consistent with the grass in the target. Although the transition seems smooth, it still not that natural.

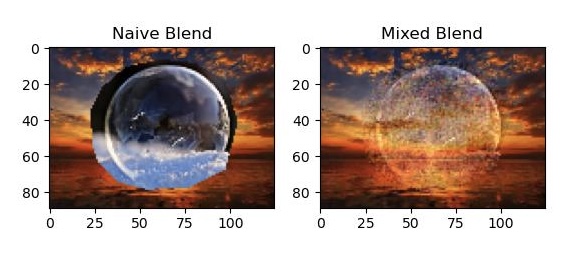
The second try is bubble with high transparency. Notice that in the center of the bubble, it is expected to reflect sunlight as show on the target image, but the Poisson Blend result got dark in the center due to the dark background on source.

source -- target

Mix Gradient

As in Poisson Blending, there are two constraints for the linear matrix function. There is only slight difference in constraint 1, where the $s_i-s_j$$s_i-s_j$ term is replaced by $\max (s_i-s_j,t_i-t_j)$$\operatorname{max}(s_i-s_j,t_i-t_j)$.

The transparency gets better now as the sunlight are visible trough the bubble. However, there comes up many annoying black noise. I think this partly because the bubble not only transmit the scenery behind but also reflect the scenery in front of it. Generally, the reflected scene tend to be ambiguous, i.e. smooth with low gradient value, but it is hard to tell which part of it transmit and which reflect, causing an uncertainty of the mixed result. Plus, low resolution makes the gradient calculation inprecise.

Appendix

Custom images source: kitty, sunset, bubble, anime grass